length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer in objects that travel at any non-zero velocity relative to that observer. This contraction (more formally called Lorentz contraction or Lorentz–Fitzgerald contraction) is usually only noticeable at a substantial fraction of the speed of light; the contraction is only in the direction parallel to the direction in which the observed body is travelling. This effect is negligible at everyday speeds, and can be ignored for all regular purposes. Only at greater speeds it becomes important. At a speed of 13,400,000 m/s (30 million mph, .0447c), the length is 99.9% of the length at rest; at a speed of 42,300,000 m/s (95 million mph, .141c), the length is still 99%. As the magnitude of the velocity approaches the speed of light, the effect becomes dominant, as can be seen from the formula:
where
L is the proper length (the length of the object in its rest frame),
L' is the length observed by an observer in relative motion with respect to the object,
v \, is the relative velocity between the observer and the moving object,
c \, is the speed of light,
and the Lorentz factor is defined as
 .
. The deviation between the measurements in all inertial frames is given by the Lorentz transformation. As the result of this transformation (see Derivation), the proper length remains unchanged and always denotes the greatest length of an object, yet the length of the same object as measured in another inertial frame is shorter than the proper length. This contraction only occurs in the line of motion, and can be represented by the following relation (where v is the relative velocity and c the speed of light)
For example, a train at rest in S' and a station at rest in S with relative velocity of v = 0.8c are given. In S' a rod with proper length L_0^{'}=30\ \mathrm{cm} is located, so its contracted length L' in S is given by:
Then the rod will be thrown out of the train in S' and will come to rest at the station in S. Its length has to be measured again according to the methods given above, and now the proper length L_0 = 30\ \mathrm{cm} will be measured in S (the rod has become larger in that system), while in S' the rod is in motion and therefore its length is contracted (the rod has become smaller in that system):
Thus, as it is required by the principle of relativity (according to which the laws of nature must assume the same form in all inertial reference frames), length contraction is symmetrical: If the rod is at rest in the train, it has its proper length in S' and its length is contracted in S. However, if the rod comes to rest relative to the station, it has its proper length in S and its length is contracted in S'.
Length contraction can simply be derived from the Lorentz transformation as it was shown, among many others, by Max Born:[6]
Length contraction can simply be derived from the Lorentz transformation as it was shown, among many others, by Max Born:[6]
Derivation
In an inertial reference frame S',  and
and 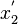 shall denote the endpoints for an object of length
shall denote the endpoints for an object of length  at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows:
at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows:
 and
and 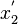 shall denote the endpoints for an object of length
shall denote the endpoints for an object of length  at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows:
at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows: and
and 
As this object is moving in S, its length L has to be measured according to the above convention by determining the simultaneous positions of its endpoints, so we have to put  . Because
. Because  and
and  , we obtain
, we obtain
 . Because
. Because  and
and  , we obtain
, we obtain- (1)

Thus the length as measured in S is given by
- (2)

According to the relativity principle, objects that are at rest in S have to be contracted in S' as well. For this case the Lorentz transformation is as follows:
 and
and 
By the requirement of simultaneity  and by putting
and by putting  and
and  , we actually obtain:
, we actually obtain:
 and by putting
and by putting  and
and  , we actually obtain:
, we actually obtain:- (3)

Thus its length as measured in S' is given by:
- (4)

So (1), (3) give the proper length when the contracted length is known, and (2), (4) give the contracted length when the proper length is known.




0 comments:
Post a Comment