Rachana Singh Thakur: De Broglie wavelength

Sunday, January 09, 2011

De Broglie wavelength

The de Broglie relations

The de Broglie equations relate the wavelength $~\lambda~$ and frequency $~f~$ to the momentum $~p~$ and energy $~E~$ , respectively, as

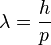$\lambda = \frac{h}{p}$ and $f = \frac{E}{h}$

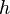where $~h~$ is Planck's constant. The two equations are also written as

$p = \hbar k$

$E = \hbar \omega$

where $~\hbar=h/(2\pi)~$ is the reduced Planck's constant (also known as Dirac's constant, pronounced "h-bar"), $~k~$ is the angular wavenumber, and $~\omega~$ is the angular frequency.
Using results from special relativity, the equations can be written as

$\lambda = \frac {h}{\gamma mv} = \frac {h}{mv} \sqrt{1 - \frac{v^2}{c^2}}$

and

$f = \frac{\gamma\,mc^2}{h} = \frac {1}{\sqrt{1 - \frac{v^2}{c^2}}} \cdot \frac{mc^2}{h}$

where $~m~$ is the particle's rest mass, $~v~$ is the particle's velocity, $~\gamma~$ is the Lorentz factor, and $~c~$ is the speed of light in a vacuum.
See the article on group velocity for detail on the argument and derivation of the de Broglie relations. Group velocity (equal to the particle's speed) should not be confused with phase velocity (equal to the product of the particle's frequency and its wavelength).

Rachana Singh Thakur

Search

Google Website Translator Gadget

Sunday, January 09, 2011

De Broglie wavelength

The de Broglie relations

0 comments:

Blog Archive