Doppler Effect

The Doppler effect (or Doppler shift), named after Austrian physicist Christian Doppler who proposed it in 1842, is the change in frequency of a wave for an observer moving relative to the source of the wave. It is commonly heard when a vehicle sounding a siren  or horn approaches, passes, and recedes from an observer. The received frequency is higher (compared to the emitted frequency) during the approach, it is identical at the instant of passing by, and it is lower during the recession.

The relative increase in frequency can be explained as follows. When the source of the waves is moving toward the observer, each successive wave crest is emitted from a position closer to the observer than the previous wave. Therefore each wave takes slightly less time to reach the observer than the previous wave. Therefore the time between the arrival of successive wave crests is reduced, causing an increase in the frequency. While they are traveling, the distance between successive wavefronts is reduced; so the waves "bunch together"





In classical physics, where the speeds of source and the receiver relative to the medium are lower than the velocity of waves in the medium, the relationship between observed frequency f and emitted frequency f0 is given by:

      

    where

      where

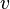is the velocity of waves in the medium

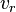is the velocity of the receiver relative to the medium; positive if the receiver is moving towards the source.

is the velocity of the source relative to the medium; positive if the source is moving away from the receiver.

The frequency is decreased if either is moving away from the other.

The above formula works for sound wave if and only if the speeds of the source and receiver relative to the medium are slower than the speed of sound





The above formula assumes that the source is either directly approaching or receding from the observer. If the source approaches the observer at an angle (but still with a constant velocity), the observed frequency that is first heard is higher than the object's emitted frequency. Thereafter, there is a monotonic  decrease in the observed frequency as it gets closer to the observer, through equality when it is closest to the observer, and a continued monotonic decrease as it recedes from the observer. When the observer is very close to the path of the object, the transition from high to low frequency is very abrupt. When the observer is far from the path of the object, the transition from high to low frequency is gradual.

In the limit where the speed of the wave is much greater than the relative speed of the source and observer (this is often the case with electromagnetic waves, e.g. light), the relationship between observed frequency f and emitted frequency f0 is given by:

Observed frequency	Change in frequency

where

is the velocity of the source relative to the receiver: it is positive when the source and the receiver are moving away from each other.

is the speed of wave (e.g. 3×10⁸ m/s for electromagnetic waves travelling in a vacuum)

is the wavelength of the transmitted wave in the reference frame of the source.

 To understand what happens, consider the following analogy. Someone throws one ball every second in a man's direction. Assume that balls travel with constant velocity. If the thrower is stationary, the man will receive one ball every second. However, if the thrower is moving towards the man, he will receive balls more frequently because the balls will be less spaced out. The inverse is true if the thrower is moving away from the man. So it is actually the wavelength which is affected; as a consequence, the received frequency is also affected. It may also be said that the velocity of the wave remains constant whereas wavelength changes; hence frequency also changes.

If the source moving away from the observer is emitting waves through a medium with an actual frequency f₀, then an observer stationary relative to the medium detects waves with a frequency f given by

where v_s is positive if the source is moving away from the observer, and negative if the source is moving towards the observer.
A similar analysis for a moving observer and a stationary source yields the observed frequency (the receiver's velocity being represented as v_r):

where the similar convention applies: v_r is positive if the observer is moving towards the source, and negative if the observer is moving away from the source.
These can be generalized into a single equation with both the source and receiver moving.

With a relatively slow moving source, v_s,r is small in comparison to v and the equation approximates to

where .

However the limitations mentioned above still apply.



Application.

1.Sirens.
2.Astronomy.
3.Temperature Measurement.
4.Radar.
5.Medical imaging and blood flow measurement.
6.Flow measurement.
7.Underwater acoustics.
ETC.....