Published by Werner Heisenberg in 1927, the principle means that it is impossible to determine simultaneously both the position and momentum of an electron or any other particle with any great degree of accuracy or certainty. It should be emphasized that this is not meant to be a statement about a researcher's ability to measure these specific pairs of quantities. Rather, it is a statement about the system itself. That is, a system cannot be defined to have simultaneously singular values of these pairs of quantities. The principle states that a minimum exists for the product of the uncertainties in these properties that is equal to or greater than one half of the reduced Planck constant (ħ = h/2π).
In quantum physics, a particle is described by a wave packet, which gives rise to this phenomenon. Consider the measurement of the position of a particle. It could be anywhere. The particle's wave packet has non-zero amplitude, meaning the position is uncertain – it could be almost anywhere along the wave packet. To obtain an accurate reading of position, this wave packet must be 'compressed' as much as possible, meaning it must be made up of increasing numbers of sine waves added together. The momentum of the particle is proportional to the wavenumber of one of these waves, but it could be any of them. So a more precise position measurement – by adding together more waves – means the momentum measurement becomes less precise (and vice versa).
The only kind of wave with a definite position is concentrated at one point, and such a wave has an indefinite wavelength (and therefore an indefinite momentum). Conversely, the only kind of wave with a definite wavelength is an infinite regular periodic oscillation over all space, which has no definite position. So in quantum mechanics, there can be no states that describe a particle with both a definite position and a definite momentum. The more precise the position, the less precise the momentum.
A mathematical statement of the principle is that every quantum state has the property that the root mean square (RMS) deviation of the position from its mean (the standard deviation of the x-distribution):
Mathematical derivations
When linear operators A and B act on a function ψ(x), they don't always commute. A clear example is when operator B multiplies x, while operator A takes the derivative with respect to x. Then, for every wave function ψ(x) we can write , so that:
, so that:For any two operators A and B:
 and
and 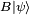 . On the other hand, the expectation value of the product AB is always greater than the magnitude of its imaginary part:
. On the other hand, the expectation value of the product AB is always greater than the magnitude of its imaginary part:Energy-time uncertainty principle
One well-known uncertainty relation is not an obvious consequence of the Robertson–Schrödinger relation: the energy-time uncertainty principle.Since energy bears the same relation to time as momentum does to space in special relativity, it was clear to many early founders, Niels Bohr among them, that the following relation holds:[2][3]

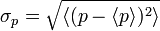

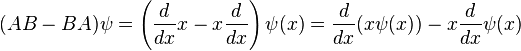


![[p,x] = p x - x p = -i\hbar \left( {d\over dx} x - x {d\over dx} \right) = - i \hbar.](http://upload.wikimedia.org/math/e/2/0/e209eb230eb1a01899da35b25da38e24.png)
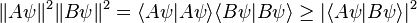

![\langle A^2 \rangle \langle B^2 \rangle\ge {1\over 4} |\langle [A,B]\rangle|^2](http://upload.wikimedia.org/math/e/a/9/ea96244c63616b1e0a3d9e7868a90223.png)

0 comments:
Post a Comment