In
quantum mechanics, the
Heisenberg uncertainty principle states by precise inequalities that certain pairs of physical properties, such as position and
momentum, cannot be simultaneously known to arbitrarily high precision. That is, the more precisely one property is measured, the less precisely the other can be measured.
Published by
Werner Heisenberg in 1927, the principle means that it is impossible to
determine simultaneously both the position and momentum of an electron or any other particle with any great degree of accuracy or certainty. It should be emphasized that this is not meant to be a statement about a researcher's ability to measure these specific pairs of quantities. Rather, it is a statement about the system itself. That is, a system cannot be
defined to have simultaneously singular values of these pairs of quantities. The principle states that a minimum exists for the product of the uncertainties in these properties that is equal to or greater than one half of the
reduced Planck constant (
ħ =
h/2π).
In quantum physics, a particle is described by a
wave packet, which gives rise to this phenomenon. Consider the measurement of the position of a particle. It could be anywhere. The particle's wave packet has non-zero
amplitude, meaning the position is
uncertain – it could be almost anywhere along the wave packet. To obtain an accurate reading of position, this wave packet must be 'compressed' as much as possible, meaning it must be made up of increasing numbers of
sine waves added together. The momentum of the particle is proportional to the
wavenumber of one of these waves, but it
could be any of them. So a more precise position measurement – by adding together more waves – means the momentum measurement becomes less precise (and vice versa).
The only kind of wave with a definite position is concentrated at one point, and such a wave has an indefinite wavelength (and therefore an indefinite momentum). Conversely, the only kind of wave with a definite wavelength is an infinite regular periodic oscillation over all space, which has no definite position. So in quantum mechanics, there can be no states that describe a particle with both a definite position and a definite momentum. The more precise the position, the less precise the momentum.
A mathematical statement of the principle is that every quantum state has the property that the
root mean square (RMS) deviation of the position from its mean (the
standard deviation of the
x-distribution):
-
-

times the RMS deviation of the momentum from its mean (the standard deviation of
p):
-
-
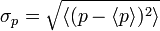
can never be smaller than a fixed fraction of
Planck's constant:
-
-

The uncertainty principle can be restated in terms of other measurement processes, which involves
collapse of the wavefunction. When the position is initially localized by preparation, the wavefunction collapses to a narrow bump in an interval Δ
x > 0, and the momentum wavefunction becomes spread out. The particle's momentum is left uncertain by an amount inversely proportional to the accuracy of the position measurement:
Mathematical derivations
When linear operators
A and
B act on a function
ψ(x), they don't always commute. A clear example is when operator
B multiplies
x, while operator
A takes the derivative with respect to
x. Then, for every wave function
ψ(x) we can write
-
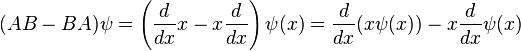

which in operator language means that
-

This example is important, because it is very close to the canonical commutation relation of quantum mechanics. There, in the position basis, the
position operator multiplies the value of the wavefunction by x, while the corresponding
momentum operator differentiates and multiplies by

, so that:
-
![[p,x] = p x - x p = -i\hbar \left( {d\over dx} x - x {d\over dx} \right) = - i \hbar.](http://upload.wikimedia.org/math/e/2/0/e209eb230eb1a01899da35b25da38e24.png)
It is the nonzero commutator that implies the uncertainty.
For any two operators A and B:
-
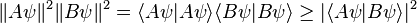
which is a statement of the
Cauchy–Schwarz inequality for the inner product of the two vectors

and
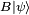
. On the other hand, the expectation value of the product AB is always greater than the magnitude of its imaginary part:
-

and putting the two inequalities together for
Hermitian operators gives the relation:
-
![\langle A^2 \rangle \langle B^2 \rangle\ge {1\over 4} |\langle [A,B]\rangle|^2](http://upload.wikimedia.org/math/e/a/9/ea96244c63616b1e0a3d9e7868a90223.png)
and the uncertainty principle is a special case.
Energy-time uncertainty principle
One well-known uncertainty relation is not an obvious consequence of the Robertson–Schrödinger relation: the energy-time uncertainty principle.
Since energy bears the same relation to time as momentum does to space in
special relativity, it was clear to many early founders,
Niels Bohr among them, that the following relation holds:
[2][3]
-










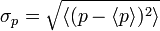

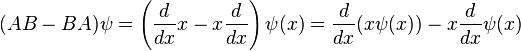


 , so that:
, so that:![[p,x] = p x - x p = -i\hbar \left( {d\over dx} x - x {d\over dx} \right) = - i \hbar.](http://upload.wikimedia.org/math/e/2/0/e209eb230eb1a01899da35b25da38e24.png)
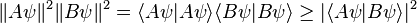
 and
and 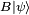 . On the other hand, the expectation value of the product AB is always greater than the magnitude of its imaginary part:
. On the other hand, the expectation value of the product AB is always greater than the magnitude of its imaginary part:
![\langle A^2 \rangle \langle B^2 \rangle\ge {1\over 4} |\langle [A,B]\rangle|^2](http://upload.wikimedia.org/math/e/a/9/ea96244c63616b1e0a3d9e7868a90223.png)


 and
and  to the momentum
to the momentum  and energy
and energy  , respectively, as
, respectively, as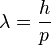 and
and 
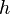 is
is 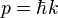

 is the reduced
is the reduced  is the
is the  is the
is the 

 is the particle's
is the particle's  is the particle's
is the particle's  is the
is the  is the
is the 


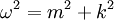
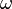 is
is 

 .
.


 and
and 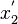 shall denote the endpoints for an object of length
shall denote the endpoints for an object of length  at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows:
at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows: and
and 
 . Because
. Because  and
and  , we obtain
, we obtain

 and
and 
 and by putting
and by putting  and
and  , we actually obtain:
, we actually obtain:
